Hvorfor og hvordan man bruger digitale filtre til konverteringer med høj opløsning, høj hastighed, analog til digital

Det er stadig en analog verden, men alligevel er digital elektronik gennemgribende og med god grund. Mens digital løser flere problemer med algoritmiske tilgange, har selv de bedste digitale algoritmer mangler, der beskæftiger sig med virkelige enheder, der findes i det analoge domæne. Dette gælder især i applikationer, der kræver dataovertagelse med høj hastighed og høj opløsning, såsom instrumentering, motorkontrol og dataopsamlingssystemer.

Problemet for designere, der ønsker at fange og behandle sådanne virkelige signaler, er behovet for at komme ind i det digitale domæne hurtigst muligt uden at gå på kompromis med denne signalinformation. Løsningen kommer fra en simpel gennemsnitsalgoritme (for at reducere støj) med et front-end analogt lavpasfilter (LPF). Med disse teknikker kan en passende enhed levere høj opløsning, høj hastighedskonvertering med indbygget analog og digital filtrering.

Denne artikel diskuterer kort de spørgsmål, der er forbundet med opnåelse af højhastighedskonverteringer med høj hastighed og med et successivt tilnærmelsesregister (SAR) analog-til-digital-konverter (ADC) ved hjælp af en analog LPF og et gennemsnitligt digitalt filter, og hvorfor denne filterkombination er en god mulighed for de fleste applikationer. Derefter introducerer den Analog DevicesAD7606C-18 otte-kanals SAR ADC og viser, hvordan man drager fordel af dens 1 megasample/s (MSPS) konverteringsfrekvens, samtidig samplingkonverterarray og fleksible digitale filterfunktioner.

For at vise, hvordan man opnår den bedste samlede præstation, kombinerer denne artikel AD7606C-18 med ADR4525 ultralav støj, høj nøjagtighed spændingsreference, også fra Analog Devices, for at forbedre den nødvendige SAR-nøjagtighed til 18-bit konverteringer.

Analoge versus digitale filtre

Hvis en analog ingeniør og digital ingeniør diskuterer filtre, kan den digitale ingeniør afvise analog. Dette ville være en fejltagelse. Filtreringsstandarden med enhver analog-til-digital (A/D) konvertering er at have den analoge LPF før det digitale filter (figur 1).

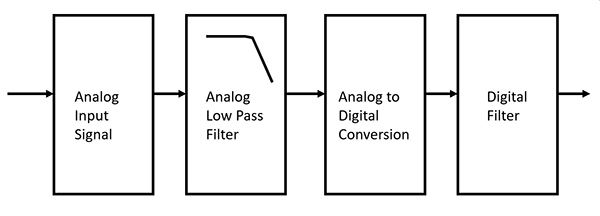Figur 1: Et blokdiagram over en analog-til-digital signalkæde med det analoge filter før det digitale filter. (Billedkilde: DigiKey)

Efter at den analoge LPF dæmper højere frekvenser over båndbredden af interesse, konverterer ADC signalet til et digitalt word. Efter denne præstation kan det digitale filter fungere på signalet inden for båndbredden af interesse.

Analoge filtre i dataopsamlingsmiljøer

Betydningen af den analoge LPF kommer til syne ved ADC's output. Ethvert signal, der passerer gennem ADC, har en størrelse og frekvens, der er forbundet med det. Ved ADC's udgang forbliver signalets størrelse den samme, hvis signalfrekvensen er under ADC's indgangsbåndbredde. Selvom A/D-konverteringen bevarer signalstørrelsen, gælder det samme ikke for signalets frekvenser. Man kan observere en ændring i frekvenserne over ½ af ADC's samplingsfrekvens, f_S, også kendt som Nyquist-samplingsfrekvensen (figur 2).

Figur 2: I graf (A) har den hurtige Fourier-transformation (FFT) repræsentation af et indgangssignal fem frekvenskomponenter. Efter en A/D-konvertering viser FFT-repræsentationen i graf (B) alle fem signaler, der forekommer under halvdelen af ADC's samplingsfrekvens (f_S). (Billedkilde: DigiKey)

I figur 2 bruger begge FFT-plot en logaritmisk frekvens på x-aksen og en lineær spænding eller størrelse på y-aksen. I graf (A) viser det analoge signal FFT-repræsentation et ADC's indgangssignal med flere signaler eller støj over halvdelen af ADC-samplingsfrekvensen, eller f_S/2.

Sammenligning af disse to grafer er det nyttigt at følge de fem FFT-signaler. Efter en ADC-konvertering forbliver det originale signals størrelser de samme, men frekvenserne over halvdelen af samplingsfrekvensen i (A) “vendes” tilbage under f_S/2 i (B). Dette fænomen er kendt som signal aliasing. For nøjagtigt at modtage signalet skal ADC's samplingshastighed f_S skal være større end to gange f_MAX hvor f_MAX er lig med signalets anvendelige båndbredde i henhold til Shannon-Nyquist-prøvetagningssætningen.

Man kan se, hvordan ADC'er permanent implanterer uønsket støj og signaler i det digitale udgangssignal. Denne ændring gør det umuligt at fortælle forskellen mellem in-band signaler og out-of-band signaler ved konverterens output.

Man kan forvente, at der er en vej frem og tilbage mellem disse to FFT-repræsentationer. Når først denne transformation er sket, er der ingen vej tilbage og fortryde den. Desværre understøtter matematik ikke denne type frem og tilbage overgang.

Tilbage til den analoge/digitale debat: et digitalt filter er utvivlsomt i stand til at anvende gennemsnits-, FIR (finite impulse response) eller uendelig impulsrespons (IIR) -filtrering og derved reducere systemstøj. Imidlertid kræver hvert digitalt filter en betydelig mængde oversampling (processen med sampling af et signal ved en samplingsfrekvens, der er væsentligt højere end den endelige outputdatahastighed), der tager tid, strøm og reducerer ADC's samplingshastighed. Den digitale filter- og konverterfunktion overvinder aldrig de aliaserede signalfænomener. Det er bedst blot at reducere den højere frekvensstøj fra starten, selv med en rudimentær analog førsteordens LPF.

Gennemsnitlige digitale filtre

SAR ADC forbedrer deres DC-støjmåling med et gennemsnitligt digitalt filter. Det gennemsnitlige digitale filter kræver flere konverteringer med en ensartet tidsskala for at øge antallet af bits. ADC-brugere bruger gennemsnitsalgoritmer med deres controller, processor eller en on-chip-gennemsnitsmotor, der fanger flere konvertersamples. Gennemsnitsprocessen "udjævner" konverteringsgruppen og forbedrer den effektive opløsning ved systemstøjreduktion.

Implementering af den konverterede dataudjævning involverer flere signaloptagelser med en konstant samplingshastighed og et gennemsnit af et forudbestemt samplingsnummer. Gennemsnitsprocessen er velkendt. Sammenfatningen af ADC-resultaterne (successive prøver, x) divideret med antallet af prøver (N) producerer en gennemsnitlig værdi (ligning 1).

 Ligning 1

Denne proces reducerer hastiheden af outputdata med en faktor N, men øger systemets afregningstid.

Standardafvigelsen for de gennemsnitlige støjende prøver (σ_gns) er standardafvigelsen for det originale signal (σ_sig) divideret med kvadratroden af N (ligning 2).

 Ligning 2

De på hinanden følgende prøver, inklusive støj, der ikke er korreleret, vil resultere i mere støjreduktion i et konstant signalgennemsnit. Hver gennemsnitlige på hinanden følgende prøve får signal-støj-forholdet (SNR) til at blive bedre, hvis signalet er DC, og støjkomponenten er tilfældig.

SNR-forbedringen er proportional med kvadratroden af antallet af gennemsnitlige prøver. Et gennemsnit på fire DC-signalsamples (4¹) øger konverterens effektive opløsning med en med en stigning på 6 decibel (dB) i SNR. A 16 eller 4² samplegennemsnit øger den effektive opløsning med to og SNR med 12 dB. Med denne logik er en gruppestørrelse på 4^N vil øge antallet af effektive bits fra en konvertering med N, hvilket bringer systemstøj til nul og SNR-værdien til uendelig.

Allan-variansen

En SNR-værdi, der svarer til uendelighed, er selvfølgelig absurd. I den virkelige verden tager erhvervelsen af det nødvendige antal prøver tid, hvorunder systemet kan ændre sig med hensyn til grader af drift.

Allan-variansen, kendt som to-prøve-varians, måler frekvensstabiliteten i en clock, oscillatorer, ADC'er og forstærkere ved at vise ændringen i støj, når antallet af prøver, der anvendes til gennemsnittet af et signal, øges. Allan-variansens statistiske analyseværktøj bestemmer det maksimale antal krævede prøver, der er optimalt for et bestemt system, hvorved stabiliteten estimeres ved at påpege frekvensdrift eller temperatureffekter.

For eksempel kan data i et system fra en ADC over tid udvise skift som vist i figur 3.

Figur 3: De 30.000 ADC-outputdatapunkter, der er fanget i løbet af ni minutter, viser en svag drift i dataene over den periode, hvilket forårsager en nedbrydning i Allan-variansberegningen. (Billedkilde: Elektronisk design)

Variansalgoritmen tager flere batcher med længere og længere gennemsnit og vurderer hvert batch resulterende støj (figur 4).

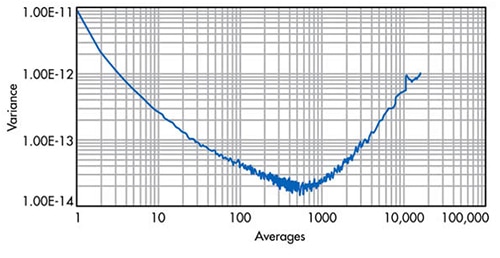Figur 4: Anvendt Allan-variansberegning for datapunkterne i figur 3. Ved 500-point-gennemsnittet erhverver dette særlige ADC-system 4,48 bits eller en 27 dB SNR-stigning. (Billedkilde: Elektronisk design)

Figur 4 demonstrerer, at den minimale varians af dette specifikke systems datapunkter forekommer ved ca. 500 ADC-output-gennemsnit - det optimale antal prøvegennemsnit til reduktion af støj. Ved 500-point-gennemsnittet erhverver dette ADC-system 4,48 bits eller en 27 dB SNR-stigning. Før og ud over det 500. gennemsnitspunkt forværres resultaterne i figur 4, da datadrift bliver en større faktor. Variabler, der påvirker Allan-variansberegningerne, kan være tid, signalstabilitet, drift, strømforsyningsvariationer og produktets ældning. Hvis et digitalt gennemsnitsfilter er i brug, er det klogt at evaluere det samlede system med Allan-variansværktøjet.

Virkelig løsning

SAR-konvertere kan tilbyde programmerbar forstærker (PGA) og digitale filterfunktioner for at forbedre den effektive opløsning og mindst signifikante bit (LSB) spænding. For eksempel er Analog Devices' AD7606C-18 en 18 bit, 1 MSPS samtidig sampling, A/D-dataopsamlingssystem (DAS) med otte kanaler, der hver indeholder analog indgangsklemme beskyttelse, en PGA, en LPF og en 18-bit SAR ADC.

Enheden har også analoge indgangsbuffere med en 1 megaohm (MW) indgangsimpedans og programmerbar ægte bipolar differentiering, bipolær single-end og unipolar single-ended indgangsspændingskonfigurationer. AD7606C-18 tillader tilslutning af otte forskellige uafhængige indgangssensorer eller signalkanaler.

AD7606C-18's digitale filter har en oversamplingstilstand, der gennemsnitlig gentager prøver fra 1 til 256 (4⁴). I henhold til Allan-variansværktøjet forbedrer denne oversampling-funktion støjydelsen ved konverterens digitale output. ADR4525 lav støjniveau, 2,5 volt præcisionsspændingsreference supplerer AD7606C-18 DAS-systemet med en del pr. Million pr. grad Celsius (ppm/°C) maksimal temperaturkoefficient og 1 mikrovolt (mV) peak-to-peak typisk outputstøj (Figur 5).

Figur 5: AD7606C-18 SAR-ADC med ADR4525 2,5 volt præcisionsspændingsreference. Induktorerne med første ordens LPF'er på V1 til V8-indgangskanalerne prøver samtidigt alle otte kanaler. (Billedkilde: Analog Devices)

Som figur 5 viser, kan denne type SAR-array med høj inputimpedans interface direkte med sensorer minus de typiske eksterne drivforstærkere. Et eksternt sensorforstærkningstrin kan også være unødvendigt. Samtidig har SAR-konverteren et internt PGA- og LPF-trin, der giver signalbehandling efterfulgt af et gennemsnitligt digitalt filter for at reducere støj yderligere ved at give højere effektive opløsninger. En sådan DAS kan tilbyde en 17,1 bit effektiv opløsning med en konverteringshastighed på 3,9 kilosampler pr. Sekund (ksps). I den anden ende af konverteringshastighedsspektret tilbyder denne enhed en 15 bit effektiv opløsning med en konverteringshastighed på 1 MSPS.

Den hurtigste konverteringshastighed på AD7606C-18 er 1 MSPS med oversampling svarende til en. Hvis konverterens kanaloversampling er to eller gennemsnit af en kanals prøver to gange, er konverteringshastigheden halvdelen af den maksimale konverteringshastighed ved 500 ksps. Til oversampling svarende til fire eller 4¹ som antallet af prøver gennemsnit, er konverteringshastigheden for den kanal 250 ksps osv. For hver af de otte kanaler tilvejebringer systemet med en oversamplingværdi på 256 et ±10 volt enkeltområde, 17,1 bit effektiv opløsning (105 dB SNR) med en konverteringshastighed på 3,9 ksps (tabel 1).

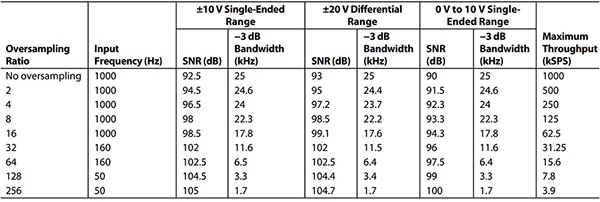Tabel 1: Ydeevne af oversampling, tilstand med lav båndbredde på AD7606C-18. (Tabelkilde: Analog Devices)

SNR til effektiv opløsning (effektivt antal bits eller ENOB) konverteringsformel vises i ligning 3.

 Ligning 3

I den anden ende af konverteringshastighedsspektret med en oversamplingsfaktor på 1 giver denne enhed 15 bit effektiv opløsning (92,5 dB SNR) med en konverteringshastighed på 1 MSPS (tabel 1).

Der er yderligere forbedringer, som AD7606C-18 tilbyder. Da der er otte separate SAR ADC'er på chip, har alle otte kanaler en samtidig samplingsfunktion. Med denne funktion er det muligt at implementere det digitale filter for at opnå høj opløsning eller høj hastighed samtidigt på alle kanaler. Derudover har alle kanaler kalibrering og diagnosticering.

For eksempel registrerer AD7606C-18's systemfasekalibrering misforholdet mellem det diskrete inputfilter. Denne værdifulde funktion identificerer enhver uoverensstemmelse på de diskrete komponenter eller i den anvendte sensor, der kan forårsage faseoverensstemmelse mellem samtidigt samplede kanaler. Enhedens softwaretilstand kompenserer fasetilpasningen pr. kanal ved at forsinke en enkelt kanals sampling øjeblikkeligt.

Systemets forstærkningskalibrering registrerer modstandsfejl ved det diskrete indgangsfilter. Denne kapacitet hjælper med at overvinde ekstern modstandsfejl. Softwaretilstanden kompenserer forstærkningsfejl pr. kanal ved at skrive den seriemodstandsværdi, der anvendes i det tilsvarende register.

Systemets offset-kalibrering rummer indgangssignalforskydningerne under kalibreringsaktiviteten. Softwaren kan justere hver kanals eksterne sensors forskydning eller enhver ekstern modstandsparts forskydning.

For en bestemt applikation skal EVAL-AD7606SDZ AD7606-kortet har software til at hjælpe med enhedsevalueringer med enhedsprogrammering samt bølgeform, histogram og FFT-optagelse (figur 6).

Figur 6: AD7606-evalueringskortet (til venstre), der er tilsluttet SDP-kortkortet (højre), hvilket gør det muligt at kontrollere evalueringskortet via USB-porten på en pc. (Billedkilde: Analog Devices)

Evalueringskortets software giver brugeren mulighed for at konfigurere hver kanals oversamplingværdi, inputområde, antal prøver og aktivt kanalvalg. Derudover gør denne software det også muligt at gemme og åbne testdatafiler.

Konklusion

På trods af et skift til digital er det stadig en analog verden, og designere har brug for analogcentreret elektronik til at løse problemer med høj opløsning og hurtig konvertering. Som vist forbedrer den enkle kombination af et analogt LPF og et digitalt gennemsnitsfilter - implementeret med det passende antal gennemsnitlige prøver - ydeevnen for en 1 MSPS SAR-konverter.